Major mathematical breakthrough went ignored

^{Thomas Royen at home in Schwalbach im Taunus (Hessen, Germany).}

Four years into his retirement, a genial insight occurred to Thomas Royen early one morning, as he was brushing his teeth: the Gaussian Correlation Inequality could be solved with the help of some of the statistical tools he had developed when he was working in the pharmaceutical industry. This was July 17, 2014. By evening, he had written down a first draft. Then he put his work aside, because, he says, "We had planned to go on a vacation, and I didn't want to spoil it for my wife." (Interview in Der Spiegel.) He nevertheless managed to find some time during these holidays, and by early August, the paper was finished. Royen was sure that he had solved a mathematical problem over which dozens, if not hundreds, of mathematicians had broken their teeth for almost sixty years. Some of them had been working on it all of fifty years. Yet, once his discovery was brought to the attention of the world, the earth did not shake. Last month - March 2017 - some of the researchers who have been struggling with the problem still ignored that the solution had been found.

Royen does not belong to breed of mathematicians who have tackled the big problems in the field. He never was invited to do research at any of the famous institutes in England, France or the USA. After he got his diploma, he went to work as a drug-trial statistician at the research laboratories of the Hoechst pharmaceuticals company, in Germany, where he was also teaching young colleagues the basics of probabilities calculations.

Later, he moved to the small Technical University at Bingen, on the banks of the Rhine, to teach mathematics – until 2010, when he went into retirement. He was a Herr Professor, but technical universities in Germany are not the place to go when you are looking for broad research programs and facilities.

Almost "as a hobby," as he puts it, Royen kept trying his hand at unsolved problems, particularly in the realm of statistics, and an area called Chi-Square-Distributions, an important tool which statisticians use to verify hypotheses, over which he had intensively reflected and to which he had contributed several papers. He had published his work in specialized publications, but he was endlessly frustrated with the delays in getting any paper read, let alone accepted. Many of his papers were turned down by peer-reviewed magazines. As far as he can tell, this happened usually without their contents having been properly examined. It appears that the readers didn't expect much that was new or interesting to come from an unknown teacher at a Technical University, and a retiree on top of it. But, as he says, he now had a lot of time at his hands...

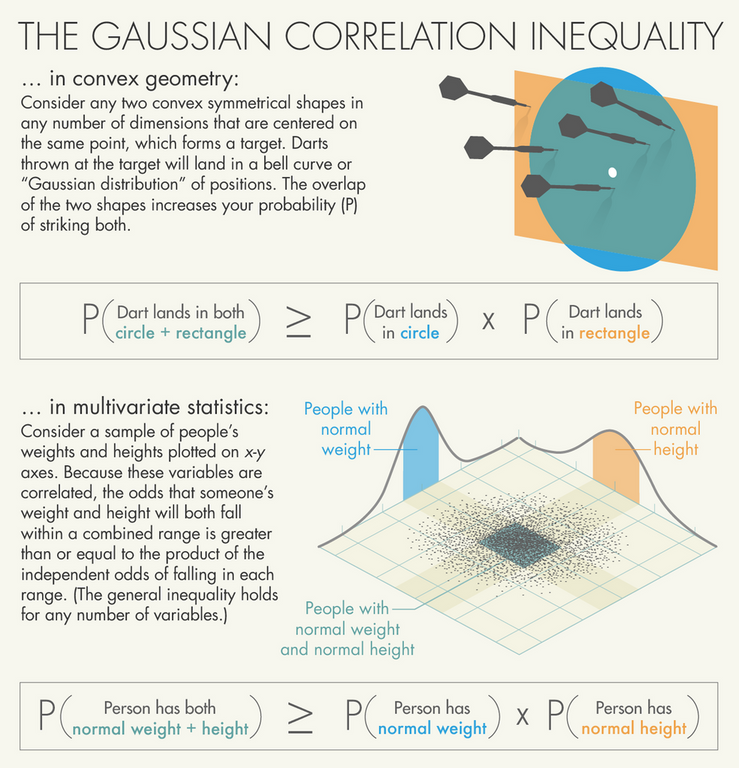
The Gaussian correlation inequality, or GCI, was conjectured in 1959 by the American statistician Olive Dunn as a formula for calculating “simultaneous confidence intervals,” or ranges that multiple variables are all estimated to fall in. It is famous in expert circles for three things: it helps with many poblems in the theory of probablilities, it can improve statistical testing procedures, and most of all – it has resisted persistently any attemps at proof for almost sixty years.

Imagine two convex polygons, such as a rectangle and a circle, centered on a point that serves as the target. Darts thrown at the target will land in a bell curve or “Gaussian distribution” of positions around the center point. The Gaussian correlation inequality says that the probability that a dart will land inside both the rectangle and the circle is always as high as or higher than the individual probability of its landing inside the rectangle multiplied by the individual probability of its landing in the circle. In plainer terms, because the two shapes overlap, striking one increases your chances of also striking the other. The same inequality was thought to hold for any two convex symmetrical shapes with any number of dimensions centered on a point.
Special cases of the GCI have been proved — in 1977, for instance, Loren Pitt of the University of Virginia established it as true for two-dimensional convex shapes — but the general case eluded all mathematicians who tried to prove it. Pitt had been trying since 1973, when he first heard about the inequality over lunch with colleagues at a meeting in Albuquerque, New Mexico. “Being an arrogant young mathematician … I was shocked that grown men who were putting themselves off as respectable math and science people didn’t know the answer to this,” he said. He locked himself in his motel room and was sure he would prove or disprove the conjecture before coming out. “Fifty years or so later I still didn’t know the answer,” he said.
Despite hundreds of pages of calculations leading nowhere, Pitt and other mathematicians felt certain — and took his 2-D proof as evidence — that the convex geometry framing of the GCI would lead to the general proof. “I had developed a conceptual way of thinking about this that perhaps I was overly wedded to,” Pitt said. “And what Royen did was kind of diametrically opposed to what I had in mind.”

Fom the article in Quanta-Magazine

Roysen had modestly written his article in Microsoft Word and posted it August 13 as a pdf on arxiv.org, an academic preprint site. Now, any highfalutin paper in mathematics or physics is supposed to be written in a software called LaTeX, and most scientific publication will not even consider anything that is not written in LaTeX.

Royen e-mailed a copy to his friend Donald Richards, a statistician from Penn State University, who checked his work and was awestruck. "I knew instantly that the problem has been solved," says Richards. "I know people who have been working on this problem for 40 years,“ he told Quanta Magazine. He himself had worked for 30 years to solve the equation – with no more results than anyone else.

Richards helped Royen to transcribe his article into LaTeX format and to get the news around, without success. Experts were dismissive to Royen’s claim that he had found the solution - it seems that they had heard it all too often before.

Royen sent his findings to the Weizmann Institute of Science at Tel Aviv University, where it arrived in a batch with two other papers on the same subject, and when the examiner found a mistake in one of them, he allegedly put the whole batch aside, "for lack of time."

Because of the poor experiences he had had with established scientific journals and publishers, Royen decided to submit his paper to an Indian journal for publication, The Far East Journal of Theoretical Statistics, which had cited him as a member of its board. There it was accepted and published – but the great institutions and universities in Europe and the US barely took notice. "In the end, it was no longer important to me that a top journal should publish my proof, but I wanted to see it published as my own idea. I no longer need high ranking magazine publications for my career, after all, I am doing this as a sort of a hobby!" Royen told the local Allgemeine Zeitung.

Finally, in December 2015 two Polish mathematicians, Rafa Lataa und Dariusz Matlak, re-published Royen's work on the arxiv.org platform, somewhat improving it for readability. After which, some mathematicians began to take notice, and the word got out.

Most startling about Royen's proof is the fact that he uses classical methods of mathematics, understandable to any student in mathematics. The proof takes all of a few pages. "A mid-level student of statistics will need maybe an hour to understand it,“ says Royen.

"So, declares Der Spiegel, with a tad of Germanic bluntlness, here was a senior Nobody finding the answer to a long elusive problem – this doesn’t happen often, in maths. Major breakthroughts usually happen in mathematicians' younger years, when they are still open for new, creative ways, and not rutted down in their choice of methods. The fact that Royen was moving at the edges of the science was probably even an advantage. He was able to attack the problem of the Gaussian Correlation Inequality with an uncluttered mind. He was not too familiar with the numerous traps and quirks which had brought other mathematicians to the edge of despair during the past decades."

Now, the world of experts is left shaking its head wondering how, in the time of digitalisation and unlimited communications, such a breakthrough could have been ignored for so long. To the quiet mirth of Thomas Royen, nearing seventy, in his retirement in Schwalbach, in the Taunus Mountains, near Frankfurt.

Anne-Marie de Grazia

Sources: Quanta Magazine (much recommended) March 28, 2017

Der Spiegel April 4, 2017

Allgemeine Zeitung April 9, 2017